编者按：九层之台，始于累土，四载潜心，方有小成。金融论文是结合现实经济活动中出现的金融问题加以研究 并将研究成果描述出来的过程。大学四年转瞬即逝，盛宝金融科技商学院又一批学子们完成了他们的高质量毕业论文。由于现实经济活动可能涉及范围较广，需考虑的因素较多，为了让金融学子们能够更好的了解我们所能学习到的知识，以及对后世大家在金融行业的造诣不断走深，在此展示盛宝金融科技商学院优秀学子们的毕业论文献礼毕业季。
毕业论文这一痛并快乐的考验，虽然青涩，却是每一位大学学子青春时代最有价值的学术起点。在毕业季到来之时，学院微信公众号将陆续推出高质量本科毕业论文集萃，通过示范、带动与辐射作用，促进各专业各年级同学交流学习。
美股游戏行业组合波动性的
GARCH模型优化策略
作者：金融科技2001李昊坤
游戏行业作为一个新兴产业，在全球范围内都具有重要的经济影响力。随着科技的不断进步和人们生活方式的改变，游戏行业在金融市场中的地位也越来越重要。因此，研究游戏行业股票的波动性对于投资者和决策者具有重要意义。
视频游戏趋势正在经历玩家和收入的大幅增长;云游戏服务专注于利用超大规模云功能、流媒体服务和全球内容分发网络来构建下一代社交娱乐平台;这些因素对市场增长产生了预期的积极影响。在游戏市场中利用云技术可能会推动多玩家对不同游戏的需求和参与度，从而在预测期内推动市场增长。游戏市场规模估计在2023年为2451亿美元，预计到2028年将达到3760.8亿美元，在预测期间（2023-2028年）以8.94%的复合年增长率增长。
GARCH模型是一种用于描述和预测金融资产如股票价格波动性的时间序列模型，本文使用GARCH模型来研究美国游戏行业股票组合的波动性。一方面是因为GARCH模型可以解释股票收益率的波动聚集效应，另一方面是因为GARCH模型可以帮助本文对美股游戏类股票的波动性进行解释和预测，本文通过试验不同GARCH模型的假设和参数，经过对比及优化后认为残差项服从正态分布的GARCH(1,1)模型拥有更好的解释和预测能力。
关键词：波动性模型分析；现代投资组合理论；金融数据分析
基于组合的GARCH模型构建与优化的实证分析
基于学生t分布的GARCH模型分析
在金融时间序列中，收益率往往表现出厚尾特性，即极端值出现的概率比正态分布预测的要高。因此，本章节假设残差也遵循学生t分布来提高模型的拟合度和预测准确性，GARCH模型假设波动率自身也具有时序依赖性,我们构建GARCH模型的目的也是检验其预测未来波动率的有效性，本文利用python中的ARCH模块来建模,其中设定均值项为常数项,波动项采用GARCH形式,ARCH项为1阶,GARCH项为1阶,即标准的GARCH(1,1)模型,图3用来描述时间序列在不同滞后阶之间的线性相关性，其公式如下所示：
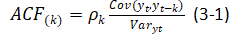
其中k代表滞阶数也后就是滞后期数k，图3的横轴也代表着滞后期数k,纵轴代表着相关系数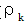 
，范围在[-1,1]之间。我们可以发现在图3中，ACF在第1阶之后快速下降到不显著水平（趋近于0），表明数据的自相关主要集中在第1阶, 这说明数据残差的方差随时间变化，并主要由当前和前一时期的残差影响,符合GARCH(1)的假设。
图3的PACF检验结果表示了时间序列数据在当前1阶时滞影响下,当前时滞的部分自相关程度(PACF),横轴为滞后期数k，纵轴为PACF系数值,范围在[-1,1]之间。我们也不难发现在图4中PACF系数值在1阶之后快速趋近于0，之后的系数值基本都落在了蓝色阴影面积内（95%的置信区间水平），表明了当前时点的值主要受上一时点影响,而不受更早时点影响, GARCH(1，1)的假设。
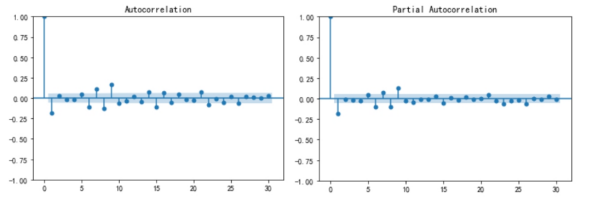
图3：ACF与PACF检验
接下来，本文在python中引入了arch模块,并定义了GARCH(1,1)模型,指定均值为常数，残差项为GARCH形式;将diss参数设置为t,表示残差服从T分布，并使用最大似然估计法对参数进行估计，模型结果如图4所示：
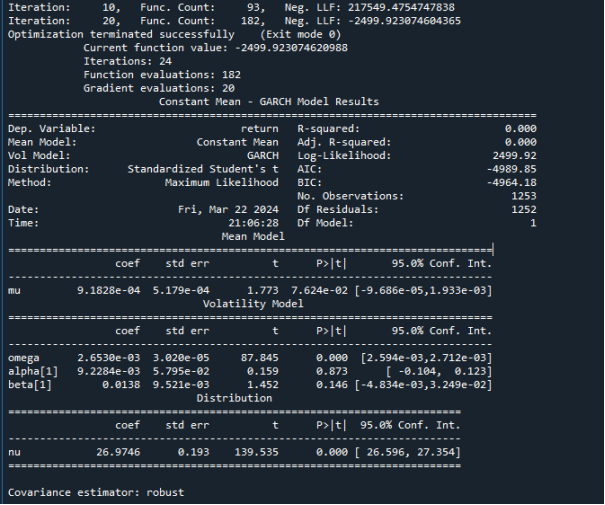
图4：服从T分布的GARCH(1,1)模型
图4表示该模型总共进行24次迭代，并对对数似然函数评估了182次。Neg.LLF表示负对数似然函数值，也就是目标函数从217549.4754下降到了-2499.923,这意味着随着迭代次数的增加目标函数值的优化收敛成功结束,得到了最小值。图中的omega表示长期波动水平。值越大,长期波动水平越高。alpha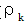反映市场异常信息对波动率的短期冲击。值越大,信息对波动率影响越大。beta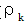反映过去波动对当前波动的影响。值越大,波动率的动态依赖性越强,这三个参数的估计值可以反映时间序列数据的波动特征。但是在模型的波动性结果中,alph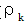a和beta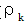的估计值都不显著,只有omega代表的基础波动率估计值结果显著，表示模型无法很好区分这三个影响因素对波动率的独立贡献。这也说明了服从T分布的GARCH(1,1)模型需要进一步优化。
优化策略1：更改残差项服从的假设分布
首先继续分析图5中的估计结果，nu代表的是自由度参数,并且理论上来说随着nu的值不断增加，标准化学生t分布的形状会越来越接近标准正态分布。第一个模型结果估算出的nu参数值约为26.9746很大,这表示使用t分布所假设的分布形状已经非常接近标准正态分布了，其实学生t分布相对于正态分布来说参数更多,模型更复杂,考虑到之前的参数估计中有个别不显著,使用更简单的正态分布可能有助于改善模型拟合。所以本文认为使用正态分布重新估计GARCH(1,1)模型的参数,可以验证t分布是否增加了不必要的复杂性,如果得出的结果表明参数都显著且好,就说明正态分布已能很好描述数据特征,不需要使用t分布模型。这将有助于简化和优化原模型。在保持其他各项参数不变的前提下，基于正态分布的GARCH(1,1)模型拟合结果如图5所示。
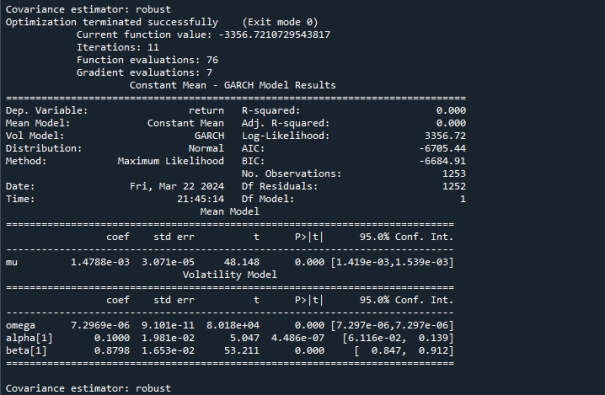
图5：服从T分布的GARCH(1,1)模型
通过对比两个模型结果与分析,本文得出以下结论：1.使用正态分布的模型的Log似然值为3356.72,使用t分布的模型值为2499.92。正态分布模型的Log似然值更高,表示它拟合数据的能力更强。2.正态分布模型的AIC和BIC值(-6705.44,-6684.91)都比t分布模型(-4989.85,-4964.18)低,说明正态分布模型在考虑复杂度情况下进行优化的效果更好。3.正态分布模型的三个波动性参数的标准误都明显下降，并且估计值均为显著。
优化策略2：调整GARCH模型的阶数
马哲光（2014）认为调整GARCH模型中的阶数，可以提高模型对波动性的捕捉能力。通常，通过比较不同模型配置的信息准则（如AIC或BIC）来选择最佳的阶数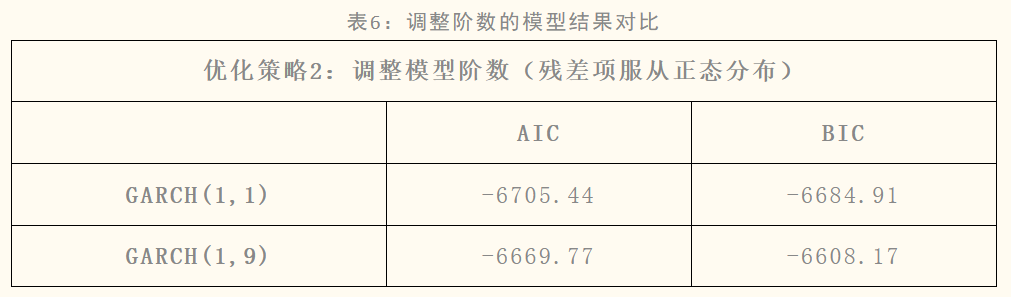
。
虽然我们从图3的PACF检验中发现 6、7、8、9阶也超过了蓝色阴影范围，但并不意味着我们必须要取到6-9阶，我认为在满足模型拟合效果的前提下，应当尽量选择更简单的模型，即阶数较低的模型。因为模型过于复杂可能会导致过度拟合，虽然多个阶数的PACF值超过了蓝色阴影范围，但1阶的PACF系数值显著大于其他阶数。这样意味着1阶的滞后期可能更重要，对模型的影响更大。通过表6可以发现GARCH(1,1)模型优化的效果更好，所以本策略无效。
优化策略3：对GARCH(1,1)引入外部变量
李姜悦、沈慈慈和王伟杰（2024）提出，通过引入外部变量（如宏观经济指标、市场信息、政策变化等），GARCH模型可以更好地解释时间序列波动性的来源，提高模型的解释能力。因为近年来美国加息频率比较高，本文将美国一年期国债利率作为外部变量引入到模型中,希望模型能够解释利率风险是否会从数据层面来影响股票的波动性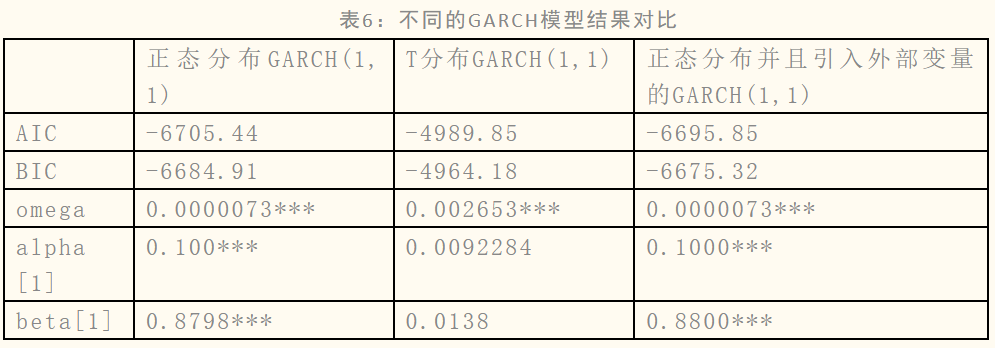
。第二列是一年期美国国债每日收益，第三列是组合每日收益，之后写入代码引入国债利率变量建模，只有国债有每日收益，将不同的模型结果进行统计，我发现正态分布GARCH(1,1)的结果是最好的，它不仅提供了最好的拟合（基于AIC和BIC），而且所有关键参数都非常显著。虽然引入外部变量的GARCH(1,1)的关键参数也显著，但其模型的拟合效果并没有第一个模型好，所以本策略被认为是无效的，也就是说国债利率并没有提高模型的解释能力。
模型有效性的验证-回溯测试
为验证结果的准确性，接下来我们用服从正态分布的GARCH(1,1)模型和服从T分布的GARCH(1,1)模型来分别预测未来5天的波动率（从数据的最后一天也就是2023年12月26日开始预测），在收集2024年1月的数据后，我们可以计算出2024.1.2-2024.1.8的实际收益率波动（实际方差）。通过实际值与预测值的比较，我们可以判断GARCH模型在优化之后的准确程度。结果如图6所示：
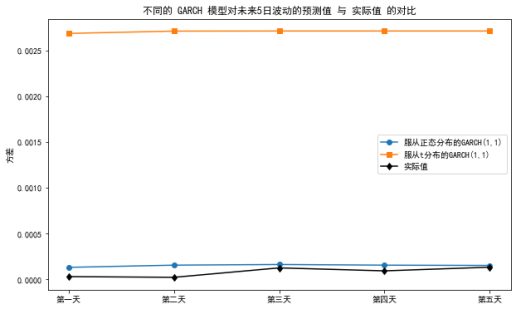
图6：不同的GARCH模型对未来5日的预测值与实际值的对比
蓝色线代表优化之后服从正态分布的模型，黄色线代表优化之前的模型。我发现经过优化之后蓝色线和实际值更加贴近。也就是说经过优化之后，服从正态分布的GARCH(1，1)模型可以更精确的预测未来5天的波动。这证明了我们的优化策略是有效的，即通过改变分布假设来提升模型的有效性。图7显示了优化之后模型的预测方差与实际方差之间的差距，经过比对，五天中有两天的结果比较贴近实际值，并且我发现预测的方差呈现的趋势与实际趋势存在一定的差别，并且实际的值有更大的波动，其实现实生活中市场波动受到多种因素影响，包括宏观经济指标、政治事件、突发事件等，这些因素如果没有被模型考虑，也可能导致预测的平滑性。通过前文可知组合中微软公司的所占比例较大为97%，2024年初微软公司成功收购了动视暴雪娱乐公司，股价出现大幅变动，所以我认为优化之后的GARCH模型并没有全部捕捉到突发事件对波动性的影响。
对于非常规的、非线性的市场影响因素，模型的预测能力受限，这也是论文存在的局限性。如果未来有机会我会继续研究改善GARCH模型来提高捕捉波动的准确性。
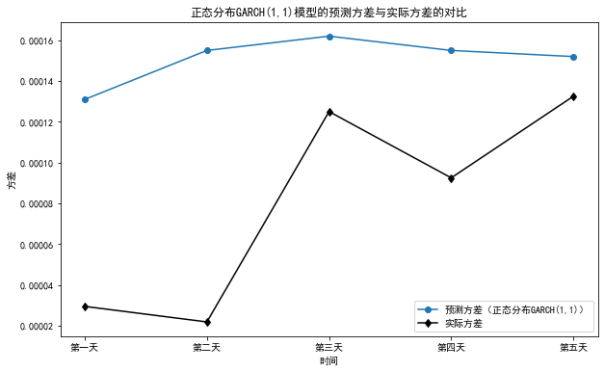
图7：正态分布GARCH(1,1)模型的预测方差与实际方差的对比